2D Gaussian

import numpy as np
import matplotlib.pyplot as plt
X, Y = np.mgrid[-10:10:100j,-9:9:99j]

from lamatrix import Gaussian2D

Gaussian2D().equation

\[f(\mathbf{y}, \mathbf{x}) = w_{0} \frac{1}{2\pi\sigma_x\sigma_y\sqrt{1 - \rho^2}} e^{- \frac{1}{2(1-\rho^2)} \left[\frac{(\mathbf{x} - \mu_x)^2}{2\sigma_x^2} + \frac{(\mathbf{y} - \mu_y)^2}{2\sigma_y^2} - \frac{2\rho(\mathbf{x} - \mu_x)(\mathbf{y} - \mu_y)}{\sigma_x\sigma_y}\right]}\]

model = Gaussian2D('x', 'y', sigma_x=2, sigma_y=2, mu_x=0, mu_y=0, rho=0.8)
w = np.random.uniform(0, 1, size=model.width)
sample = model.design_matrix(x=X, y=Y).dot(w)

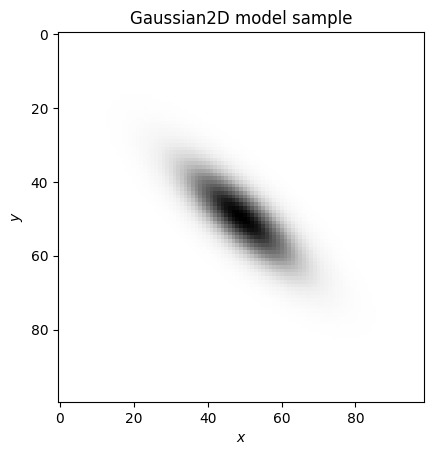
fig, ax = plt.subplots()
ax.imshow(sample, cmap='Greys')
ax.set(xlabel='$x$', ylabel='$y$', title='Gaussian2D model sample');