Sinusoid

lamatrix provides a Sinusoid model which can be used to capture periodic variability. This model enables you to fit for the amplitude of sinusoids, but is not linear in the period of the sinusoid.

import numpy as np
import matplotlib.pyplot as plt
x = np.arange(-10, 10, 0.01)


from lamatrix import Sinusoid

Sinusoid(nterms=1).equation

\[f(\mathbf{x}) = w_{0} \sin(\mathbf{x}) + w_{1} \cos(\mathbf{x})\]

As shown above, this is only linear in the amplitudes of the sine and cosine terms. There is no way to build a linear model where a multiplicative weight can govern the period of these functions.

lamatrix also provides a way to increase the number of terms of this model to fit higher order variability

Sinusoid(nterms=2).equation

\[f(\mathbf{x}) = w_{0} \sin(\mathbf{x}) + w_{1} \cos(\mathbf{x}) + w_{2} \sin(2\mathbf{x}) + w_{3} \cos(2\mathbf{x})\]

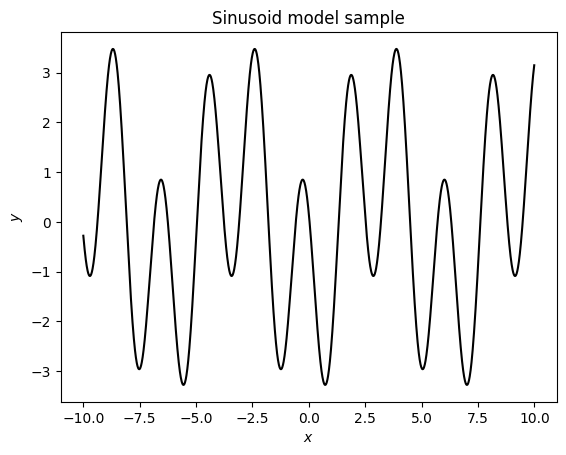
model = Sinusoid('x', nterms=3)
w = np.random.normal(size=model.width)
sample = model.design_matrix(x=x).dot(w)

fig, ax = plt.subplots()
ax.plot(x, sample, c='k')
ax.set(xlabel='$x$', ylabel='$y$', title='Sinusoid model sample');